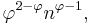Golomb sequence

In mathematics, the Golomb sequence, named after Solomon W. Golomb (but also called Silverman's sequence), is a non-decreasing integer sequence where a_n is the number of times that n occurs in the sequence, starting with a₁ = 1, and with the property that for n > 1 each a_n is the unique integer which makes it possible to satisfy the condition. For example, a₁ = 1 says that 1 only occurs once in the sequence, so a₂ cannot be 1 too, but it can be, and therefore must be, 2. The first few values are

1, 2, 2, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 8, 8, 8, 8, 9, 9, 9, 9, 9, 10, 10, 10, 10, 10, 11, 11, 11, 11, 11, 12, 12, 12, 12, 12, 12 (sequence A001462 in OEIS).

Colin Mallows has given an explicit recurrence relation a(1) = 1; a(n + 1) = 1 + a(n + 1 − a(a(n))). An asymptotic expression for a_n is

$\varphi^{2-\varphi}n^{\varphi-1},$

where φ is the golden ratio.

References

Richard K. Guy, Unsolved Problems in Number Theory (3rd ed), Springer Verlag, 2004 ISBN 0-387-20860-7; section E25.